Bitműveletek

Az előző cikkben sajnálatomat fejeztem ki annak kapcsán, hogy a legtöbb programozó nem veszi a fáradtságot, hogy bitműveletekkel bíbelődjön.

Felmerülhet a kérdés, hogy ha amúgy sem fogom használni akkor minek beszélni róla. Azt azért szögezzük le, hogy valamit nem használni és egyáltalán nem is tudni róla az két külön dolog. Biztos vagyok benne, hogy a BMW-sek is tudják mi az az index csak éppen használni nem szokták (elnézést az általánosításért, és a kivételektől itt a zárójelen belül kérek elnézést).

A bitműveletek azon kevés utasítások közé tartoznak, melyet a legtöbb CPU natívan megért, ezért ezek a műveletek nagyon gyorsan hajtódnak végre.

Logikai bitműveletek:

• NOT: (magyarul: nem) egy olyan művelet, melynek egy bemenő paramétere van (unary operator). Ennek minden bitjén logikai negálást (megcseréljük a biteket: 0-ból 1 lesz és 1-ből pedig 0) hajtunk végre. Példa a NOT műveletre:
  NOT 0111 = 1000
• AND: (magyarul: és) egy olyan művelet, ahol két egyforma hosszúságú (8 bit, 16 bit, 32 bit, 64 bit, stb) bináris számon az egymással azonos helyiértéken lévő biteken (azaz bitenként) logikai AND műveletet hajtunk végre. Az eredmény a bitek egymáshoz való viszonyából a következő lehet:
  - 0, ha a két bit bármelyike 0 volt
  - 1, ha mindkét bit 1 volt
  Példa az AND műveletre:
  0101 AND 0011 = 0001
• OR: (magyarul: vagy) egy olyan művelet, ahol két egyforma hosszúságú bináris számon az egymással azonos helyiértéken lévő biteken logikai OR műveletet hajtunk végre. Az eredmény a bitek egymáshoz való viszonyából a következő lehet:
  - 0, ha mindkét bit 0 volt
  - 1, ha bármelyik bit 1 volt
  Példa az OR műveletre:
  0101 OR 0011 = 0111
• XOR (eXclusive OR): (magyarul: kizáró vagy) egy olyan művelet, ahol két egyforma hosszúságú bináris számon az egymással azonos helyiértéken lévő biteken logikai XOR műveletet hajtunk végre. Az eredmény a bitek egymáshoz való viszonyából a következő lehet:
  - 0, ha mindkét bit 0 volt VAGY mindkét bit 1 volt
  - 1, ha a két bitből az egyik 1 volt, míg a másik 0
  Példa a XOR műveletre:
  0101 XOR 0011 = 0110

Az AND, OR és XOR úgznevezett binary operator, mert két bemenő értékkel dolgoznak. Létezik még a ternary, amely pedig hárommal, de arról majd kicsit később lesz szó.

Bit eltoló műveletek (még a logikai bitműveleteknél is ritkábban használtak, ne ess pánikba, ha elsőre, másodikra vagy akár hatodszorra is soknak találod az itt leírtakat):
A különböző hosszúságon ábrázolt bináris számok jobbra vagy balra való eltolását valósíthatjuk meg ezekkel az utasításokkal. Három fő típusa létezik, az arithmetic (aritmetikai: a matematikának az az ága, amely az összeadás, a kivonás, a szorzás és az osztás műveleteivel foglalkozik), logical (logikai) és circular vagy rotate (körkörös). Mivel a számoknak fix hosszúsága van az LSB-t és az MSB-t a tolás irányától és típusától függően különbözőképpen kezeljük.

• arithmetic: azok a bitek amik a tolás következtében kitolódnak jobbra vagy balra, azok elvesznek (...). Balra tolásnál 0 lép be a jobb oldalon (ő lesz az új LSB). Jobbra tolásnál a sign bit (MSB illetve kettes komplemensnél előjel bit, ahogy az előző leckében megtanultuk) balról bekerül (így ő veszi át az előjelbit szerepét és megőrízzük a szám előjelét).
  Példa: 00010111 LEFT-SHIFT = 00101110
  A balra és jobbra tolások 2-vel való szorzásnak illetve osztásnak felelnek meg. (ellenőrizd számológéppel, hogy a fenti példánál a kapott szám valóban 2x annyi, mint a tolás előtt)

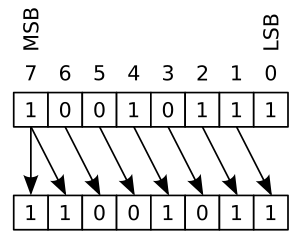
• logical: ebben az esetben mindig 0 kerül be az MSB vagy LSB helyére. Mivel balra tolásnál ez az aritmetikai esetében is így van, ezért balra tolás esetében nincs különbség köztük. Jobbra tolás esetén azonban célszerű a logikai tolást használni ha nem akarunk kettes komplemenssel dolgozni, hanem csak pozitív számokkal

• circular: ennek két fajtája van az úgynevezett no carry és a carry változat. No carry esetén a kitolódó bit a másik oldalon belép, míg a carry-s változat esetén a kilépő bit bekerül egy átmeneti 1 bites tárolóba (ez a carry), míg a carry előző tartalma bekerül a belépő olalon.

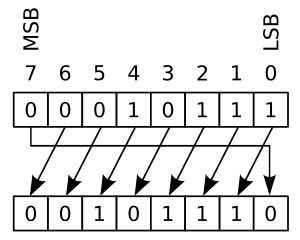
Mégegyszer: 2-es számrendszerben az eltolás, 2-vel való szorzást/osztást eredményez. Ez egyébként minden számrendszerben így van, pl. a 10-es számrendszerben ha a 121-et "eltolod" balra és jobbról hozzáraksz egy 0-át, akkor 10-el szoroztál, míg jobbra tolásnál 10-el osztottál. Tehát általánosságban elmondható, hogy a számrendszer alapszámával való szorzás/osztás történik. Azon "apróságtól", hogy a toláskor elvesző helyiértéken lévő 0-tól különböző szám esetében az osztás nem lesz pontos, egyelőre tekintsünk el.

Ez most biztosan nagyon száraz volt, de ahogy előzőleg írtam is, ez az a rész, amit nagy valószínűséggel nem nagyon fogsz használni. Szerencsére elég sok fordító fel van készítve arra, hogy ha pl. egy 2-vel való szorzást talál a kódodban, akkor kioptimalizálja neked bit eltoló műveletté, de ha esetleg olyan nyelven írsz programot ahol ez nem így van akkor sem kell túl sokat törnöd rajta a fejed.

Mit tanultál ebben a leckében?

• logikai bitműveleteket, melyek egy (unary) vagy két bemenő számon bitenként végeznek műveletet
• bit eltoló műveleteket, melyek jobbra vagy balra tolják (léptetik) az egyes biteket
• mind a logikai mind a bit eltoló műveletekkel elég masszívan meg lehet változtatni a számokat és ha nem veszett még el benned a matematikus, akkor talán még érdekesnek is találtad